$$(a, b, c)×(x, y, z)=(bz-cy, cx-az, ay-bx)$$
計算例を挙げてみると…
$$(1, 2, 3)×(1, 4, 9)=(6, -6, 2)$$
ベクトルの外積の場合、掛ける順序を逆にすると得られるベクトルが逆向きになります。
$$(1, 4, 9)×(1, 2, 3)=(-6, 6, -2)$$
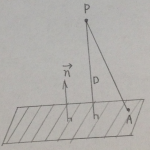
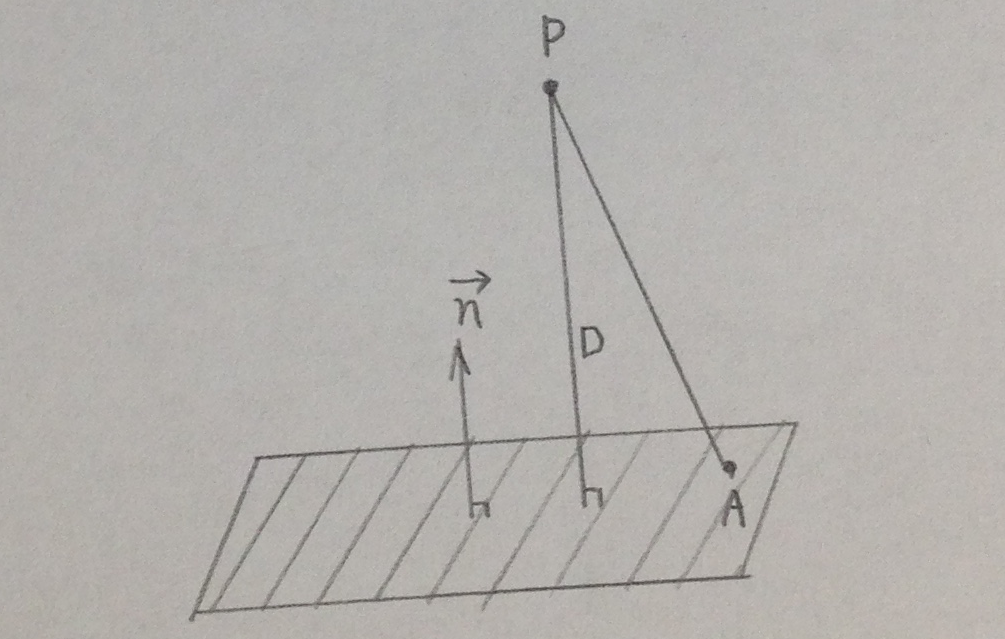
外積は平面と点の距離の計算など、便利な応用が多数あります。なお、外積の大きさは2つのベクトルの作る平行四辺形の面積と等しくなっています。なお、ベクトル1の進む方向を向いて見るとベクトル2から見て時計回りの方向に外積は伸びていきます。

OpenCVのPoint3f型は3次元の点の座標を保持する型であると同時に、ベクトルを表現することもできます。OpenCVを使った外積を計算する関数は以下のように書けます。
Point3f cross(Point3f v1, Point3f v2){
return Point3f((v1.y * v2.z) - (v1.z * v2.y), (v1.z * v2.x) - (v1.x * v2.z), (v1.x * v2.y) - (v1.y * v2.x) );
}
もちろんOpenCVには組込みの外積計算があります。この場合はベクトル専用のVec3f型を使う必要があります。cross関数を使います。内積もdot関数で求められます。
Vec3f v1(1,2,3);
Vec3f v2(4,5,6);
Vec3f n = v1.cross(v2);
double dot = v1.dot(v2);