二次元での拡散シミュレーションをコーディングしましたが、今回は三次元版です。最後にソースコードを載せてあります。二次元版では100×100のグリッド密度で計算しましたが、三次元版では100×100×100にすると配列にしたときに必要になるメモリが大きすぎてエラーが出るだろうと思いましたので、50×50×50にしています。
空間内への各場所の濃度φは極座標によってφ(r,θ,ψ)と表せます。今回は境界条件をr<0.08で濃度1.0、r>0.50で濃度0.0としたので、濃度分布は球対称となり、φ(r)と書きなおすことができます。解析的に定常解が求まる例なので、先に解析解を求めます。△はラプラシアンです。
拡散方程式は、∂φ/∂t=D△φ と表されます。
定常解とは時間の変化があっても変化しない濃度分布のことであるので、∂φ/∂t=0が成り立ちます。すなわち、方程式D△φ=0が解ければ良いということになります。ここでDが定数の時には簡単にこれを解くことができます。
まず、三次元極座標のラプラシアンに以下の公式があります。
△=∂2/∂x2+∂2/∂y2
=(∂2/∂r2)+1/r2(∂2/∂θ2)+1/(r2 sin2θ)(∂2/∂ψ2)+2/r(∂/∂r)+cos θ/(r^2sinθ)(∂/∂θ)
これを元に、φがθによらないこと、
すなわち∂φ/∂θ=∂2φ/∂θ2=∂2φ/∂ψ2=0であることに注意して、
△φ=(∂2φ/∂r2)+2/r*(∂φ/∂r)=0
すなわち
∂2φ/∂r2=-2/r*(∂φ/∂r)
∂φ/∂rは微分すると-2/r倍のそれになる関数とわかり、
∂φ/∂r=A/r2
これをrで積分して
φ=A/r +B
ここに境界条件 φ(0.08)=1,φ(0.50)=0 を代入してA=-0.095 B=-0.19と求まります。
それでは、この解析解を用いてシミュレーションによって得られた定常解を検証していきます。シミュレーションですが、二次元版と比べると50^3/100^2=12.5倍の負荷がかかっています。30万タイムステップで収束としました。
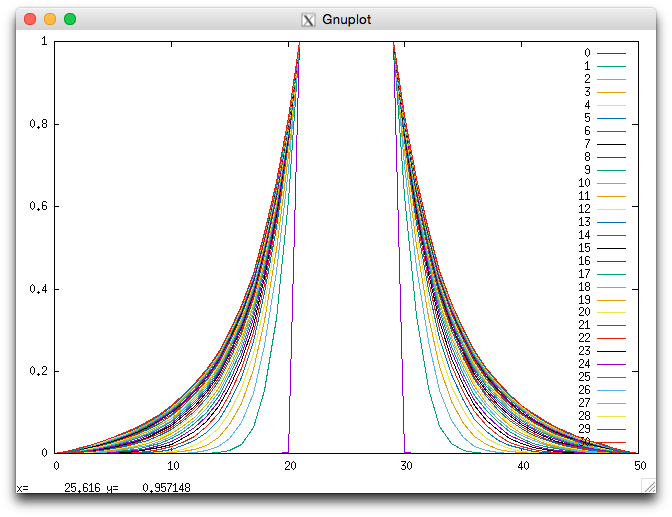
濃度分布の経時変化です。球の直径上における濃度です。
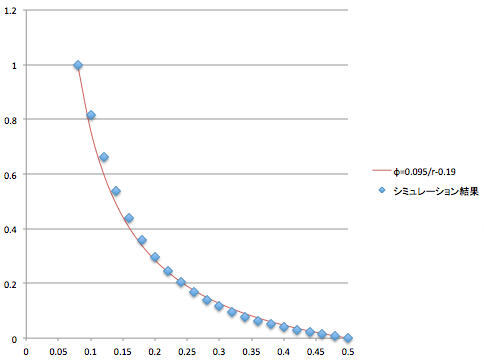
解析解とシミュレーション結果の比較。ほぼ理論値通りです。
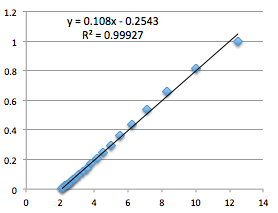
x=1/rと変換して一次式近似しました。
解析解とうまく一致したので、解析解を導くのが難しい場合には、このプログラムが活躍できるということですね。最後にソースコードを載せておきます。
#include <iostream>
#include <stdio.h>
#include "opencv/cv.h"
#include "opencv/highgui.h"
#define NMAX_X 50
#define NMAX_Y 50
#define NMAX_Z 50
#define N 2000000
double r(double,double,double,double,double,double);
double f3(double,double,double,int);
int main(){
char *output ="noudo.txt";
FILE* fpo;
fpo=std::fopen( output, "w" );
cv::Mat img=cv::Mat(cv::Size(NMAX_X,NMAX_Y),CV_8UC3);
cv::namedWindow("img", CV_WINDOW_AUTOSIZE);
int i,j,k,w,p;
double ax,ay,az,dx,dy,dz,dt,a;
double U[NMAX_X+1][NMAX_Y+1][NMAX_Z+1],UU[NMAX_X+1][NMAX_Y+1][NMAX_Z+1];
double MaxValue;
dt=1.0/1000000.0;
dx=1.0/(double)NMAX_X;
dy=1.0/(double)NMAX_Y;
dz=1.0/(double)NMAX_Z;
a=1.0/1.0;
ax=1.0/dx/dx;
ay=1.0/dy/dy;
az=1.0/dz/dz;
FILE* gp;
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
for(k=0;k<=NMAX_Z;k++){
U[i][j][k]=f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,(double)k/(double)NMAX_Z,5);
UU[i][j][k]=0.0;
}
}
}
gp = popen("/usr/local/bin/gnuplot -persist","w");
fprintf(gp, "set terminal x11\n");
for(w=0;w<=N;w++){
if(w%1000==0){
img=cv::Scalar(0,0,0);
MaxValue=0;
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
//for(k=0;k<=NMAX_Z;k++){
if(MaxValue<U[i][j][NMAX_Z/2])MaxValue=U[i][j][NMAX_Z/2];
//}
}
}
for(i=0;i<=NMAX_X;i++){
for(int j=0;j<NMAX_Y;j++){
//for(k=0;k<=NMAX_Z;k++){
p = (int)img.step*((int)j)+(((int)i)*3);
img.data[p+1] =((int)(U[i][j][NMAX_Z/2]*255/MaxValue))%256 ;
//}
}
}
cv::imshow("img", img);
if(cv::waitKey(1)!=-1){
fclose(fpo);
pclose(gp);
return 0;
}
}
printf("%d\n",w);
for(i=1;i<=NMAX_X-1;i++){
for(j=1;j<=NMAX_Y-1;j++){
for(k=0;k<=NMAX_Z;k++){
UU[i][j][k]=a*dt*(ax*U[i+1][j][k]+ax*U[i-1][j][k]+
ay*U[i][j+1][k]+ay*U[i][j-1][k]+
az*U[i][j][k+1]+az*U[i][j][k-1])+
(1.0-2.0*a*dt*(ax+ay+az))*U[i][j][k];
}
}
}
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
for(k=0;k<=NMAX_Z;k++){
U[i][j][k]=UU[i][j][k];
}
}
}
for(i=NMAX_X/2-4;i<=NMAX_X/2+4;i++){
for(j=NMAX_Y/2-5;j<=NMAX_Y/2+5;j++){
for(k=NMAX_Z/2-5;k<=NMAX_Z/2+5;k++){
if(f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,(double)k/(double)NMAX_Z,5))U[i][j][k]=1;
}
}
}
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
for(k=0;k<=NMAX_Z;k++){
if(!f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,(double)k/(double)NMAX_Z,25))U[i][j][k]=0;
}
}
}
if(w%1000==0){
for(int ro=0;ro<=NMAX_X;ro+=1){
fprintf(fpo, "%d %f\n",ro,U[ro][(int)NMAX_Y/2][(int)NMAX_Z/2]);
printf( "%d %f\n",ro,U[ro][(int)NMAX_Y/2][(int)NMAX_Z/2]);
}
fprintf(fpo, "\n\n");
fflush(fpo);
fprintf(gp, "plot ");
for(int i=0; i<=w/1000;i++){
fprintf(gp, "\"noudo.txt\" index %d using 1:2 title \"%d\" with lines,",i,i);
}
fprintf(gp, "\n");
fflush(gp);
}
}
fprintf(gp, "\n");
pclose(gp);
fclose(fpo);
}
double r(double x1,double y1,double z1,double x2,double y2,double z2){
return pow((pow((x1-x2),2)+pow((y1-y2),2)+pow((z1-z2),2)),0.5);
}
double f3(double x,double y,double z,int rr){
if(r(x*50,y*50,z*50,25,25,25)<rr) return 1;
else return 0;
}