NumPyを使うと簡単に二次元配列を作ることができます。ここでは、NumPyのzeros関数を使って要素が全てゼロの配列を作っています。 import numpy as np array2d = np.zeros((4,…

今回はPythonで細胞数のカウントをしてみます。C++での粒子カウントを解説したものはこちらになります。 ヒト臍帯静脈内皮細胞 (HUVEC) CD31 の免疫蛍光染色　200× コスモバイオ 画像のチャンネル分離 c…

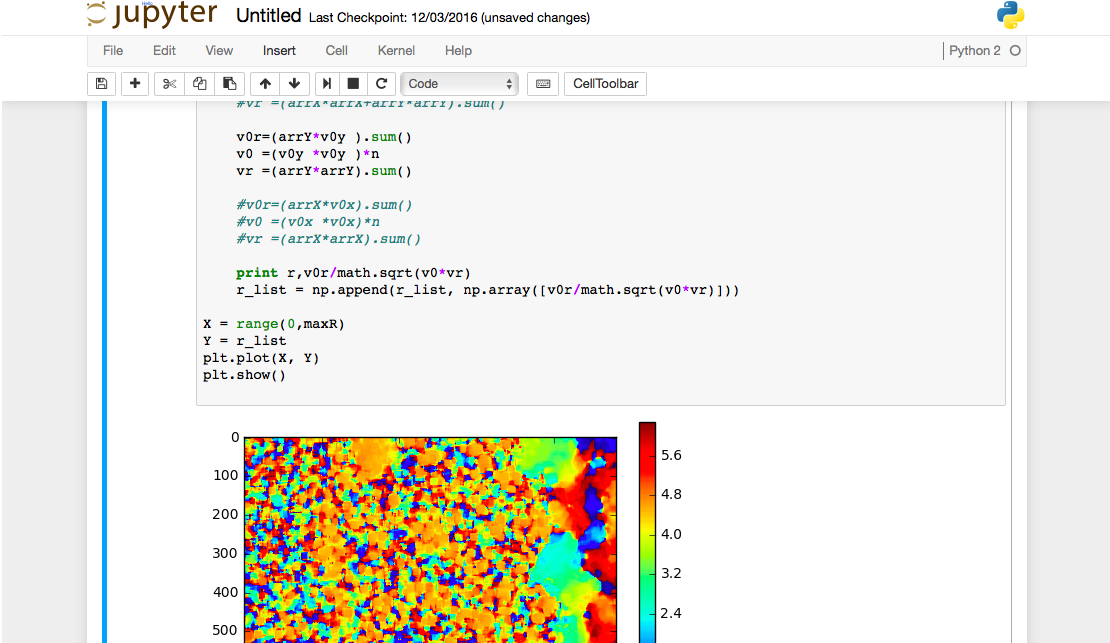
このページではPythonの基本的な使い方を紹介します。 Jupyter notebookを起動する まず、Pythonの環境構築をした時に、pyenvを使った場合にはその環境に入ります。次に、Jupyter noteb…

MacまたはLinuxでは次のようにしてGPUによるアクセラレーションが有効なChainer環境を構築できます。GPU版のインストールには対応したGPUが必要になるので、準備が必要です。なお、私が使っているGPUはGeF…

MacまたはLinuxでは次のようにしてChainer環境を構築できます。GPUが使える環境では、計算速度が数十倍〜数百倍になる、こちらで解説しているインストール方法がお勧めです。 まず、Pythonの環境構築をした時に…

MacまたはLinuxでは次のようにコマンドを打つことでPythonとJupyterの環境を構築できます。インストール後のPythonの基本的な使い方はこちらに書きました。Pythonはバージョン2系と3系があり、少し書…

画像から種子の数をカウントします。解析の種類としては、一般的には粒子解析と言われます。光の当たり方にムラのある条件でも可能な2値化手法など応用的な内容も含んでいますが、まず初めに実施してみてほしい簡単なチュートリアルです…

今回は干潟を斜め上の角度から撮影した画像をオリジナル画像とし、ホモグラフィー変換によって真上から撮影したような形状に変形する例を紹介します。 平面の変形方法にはいくつか種類がありますが、透視変換（ホモグラフィー変換）は最…

[mathjax] 移動体の追跡や粒子のカウントのチュートリアル中では輪郭構成点から近似的な中心座標を求める手法を紹介していましたが、今回は厳密な重心を求める手法を紹介します。まずは重心の定義から見ていきましょう。なお、…

C++とOpenCVを使ってフーリエ変換を行います。フーリエ変換はJPEGの圧縮にも使われる技術ですが、ノイズの除去などにも応用が可能です。 まず、フーリエ変換についてですが、フーリエ変換は元の画像あるいは波形から、それ…