反時計回りに角度θだけ回転させる回転行列は $$\begin{eqnarray} R(\theta) = \left( \begin{array}{cc} ~\cos \theta & -\sin \theta…

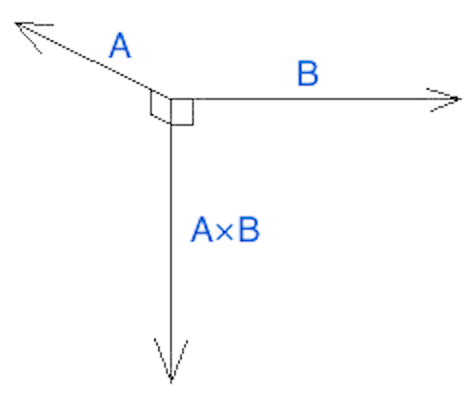
3次元空間上の3点A,B,Cが与えられたとき、この3点で囲む三角形の面積を求めます。実はこれはベクトルの外積を使うと簡単に計算できます。 まずベクトルABとACを計算します。ベクトルの外積の大きさは外積の計算に用いた2つ…

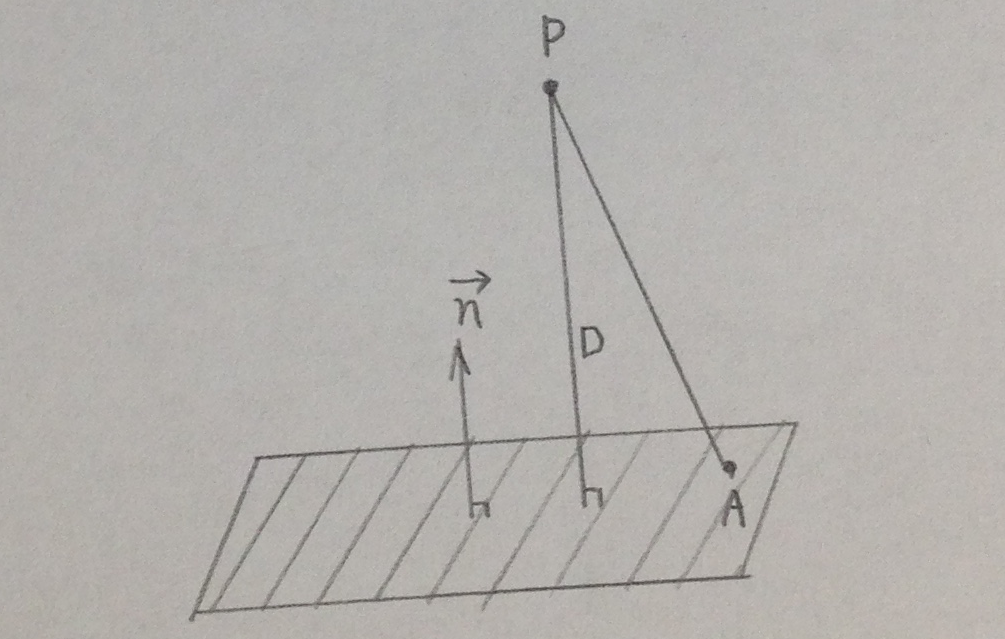
距離の公式 次の平面と点Pが与えられたとき、 $$ax+by+cz+n=0 \\ P (x_{0},y_{0},z_{0})$$ 平面との距離Dは以下の式により求められます。 $$D=\frac{|ax_{0}+by_{…

3次元ベクトルの外積は次のように定義されます。 $$(a, b, c)×(x, y, z)=(bz-cy, cx-az, ay-bx)$$ 計算例を挙げてみると… $$(1, 2, 3)×(1, 4, 9)=…

二次元での拡散シミュレーションをコーディングしましたが、今回は三次元版です。最後にソースコードを載せてあります。二次元版では100×100のグリッド密度で計算しましたが、三次元版では100×100×100にすると配列にし…

数値Aの符号を返す関数が必要になった時、どのような方法があるでしょうか。ぱっと思いつく範囲では、「if 文で条件分岐」か「AをAの絶対値で除算する」くらいだと思います。 C++で書くならば double sign(dou…

二次元平面上での物質の拡散をシミュレーションしました。三次元版はこちらにあります。 時間の経過とともにどのように物質濃度の分布が変化するかを計算します。その時に、現在の状態から⊿ｔだけあとの分布の状態を求めます。差分近似…

楕円は円錐を平面で切ったときにできる図形のうちの1つです。今回は楕円の周の長さCを数値計算によって求めます。長軸2a、単軸2bのx2/a2+y2/b2=1で表される楕円の面積はπabと簡単に計算できますが、楕円の周の長さ…

Zhang-Suenの細線化アルゴリズムを紹介します。このアルゴリズムは2値画像を細線化するもので、8近傍を持つ全てのピクセルに対して2つの処理X、処理Yを連続して行います。 まず、次のような3*3のます目を考えます。中…