流体力学シミュレーションによる材料構造評価 – 絶対浸透率と固有浸透テンソル、曲路率
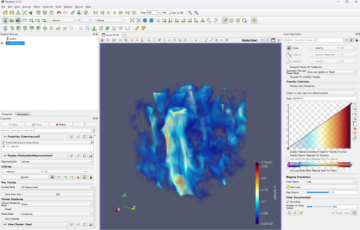
流体力学シミュレーションの材料評価への応用 材料の特性を測定する方法のひとつとして、流体がどれだけ通り抜けやすいか、というものがあります。測定には、実際に水や空気、油などの透過性を実験で測定する方法もありますが、X線CT…
 数学とアルゴリズム
数学とアルゴリズム
流体力学シミュレーションの材料評価への応用 材料の特性を測定する方法のひとつとして、流体がどれだけ通り抜けやすいか、というものがあります。測定には、実際に水や空気、油などの透過性を実験で測定する方法もありますが、X線CT…
 Python 応用編
Python 応用編
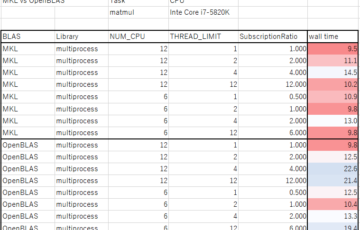
Pythonでは基本的に、Global Interpreter Lockといって、一つのプロセスでしか動かせない、という制約がある。これは、複数スレッドを立ち上げてPythonコードを実行しようとしても、CPUでの計算を…
 Python
Python
自分用のメモです。回転同士の距離がどういうものか、といったことはここに日本語で詳しく書いてあります(とても良いページ!)。 from pyquaternion import Quaternion import numpy…
 Python
Python
はじめに 3次元回転(金谷健一著)を読んで、あるコスト関数を最小化するための3次元回転の最適化について、リー代数の方法、の理論的なところを少なくとも一部理解したので、実際に実装してみようというのが今回の目的。 リー代数と…
 Python
Python
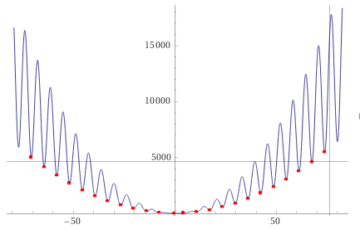
Scipyによる最適化計算 Pythonで最適化計算を行う場合、Scipyのoptimizationパッケージを使うことになると思う。これには、いろいろな最適化アルゴリズム(Nelder-Mead, Powell, BF…
 Python
Python
クロフトンの公式 CTなどのボリュームデータにおいて、何らかの方法でセグメンテーションを行ったあと、そのラベルデータの表面積を計算したいときがあります。このとき、クロフトンの公式というものを使うと正確に計算できます。これ…
 Python
Python
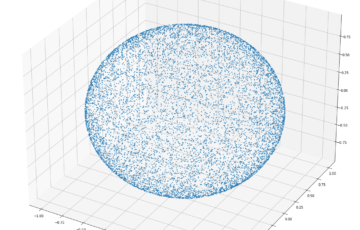
方針 簡単のために単位球を考えます。乱数tで緯度を決め、乱数uで経度を決めます。ただし、緯度ごとに、緯線の長さが異なるため、球面上に均一に分布させるために、この緯線の長さに比例した頻度でtを生成する必要があります。 なお…
 Python
Python
Pythonでの生成方法を書いていきますが、根底にある考え方は他の言語でも共通です。 手始めに、一様乱数から 確立密度関数で表現すると、[0, 1)において、P(x) = 1。 # [0, 1)の乱数を生成 import…
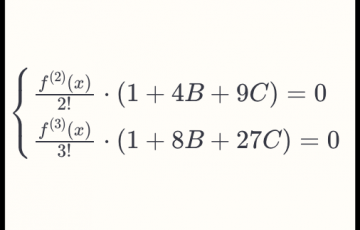 数学とアルゴリズム
数学とアルゴリズム
解析解(数学解)が求められない場合に、数値解析で数値解を計算するが、計算機で扱うためには離散化が必要である。ここでは、微分方程式を解く時に必要な離散化を考える。 微分方程式を解くための離散化には、時間の離散化と、空間の離…
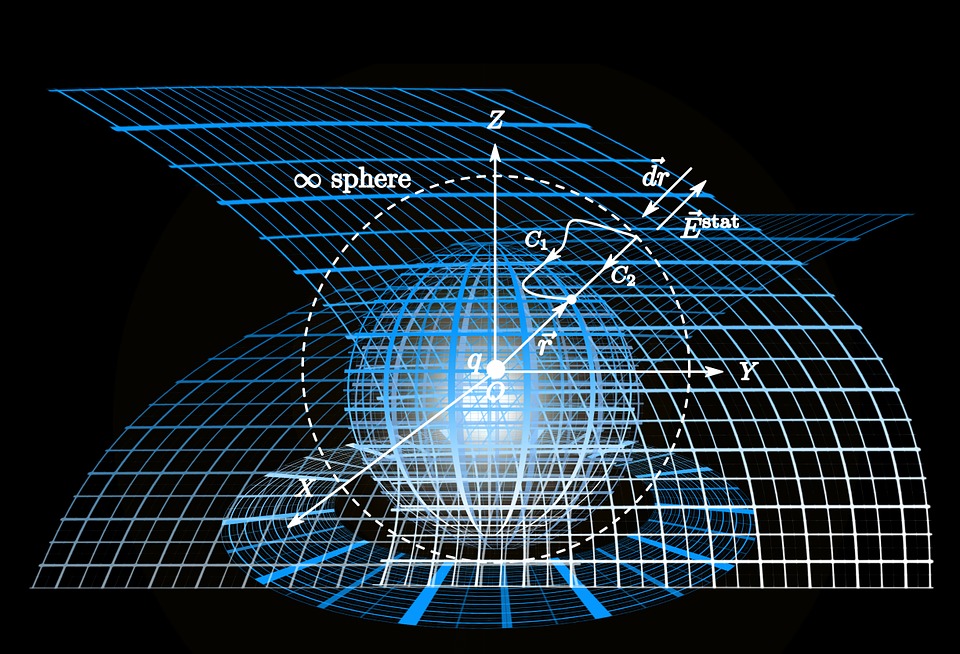 C++ 計算幾何
C++ 計算幾何
[mathjax] 反時計回りに角度θだけ回転させる回転行列は $$\begin{eqnarray} R(\theta) = \left( \begin{array}{cc} ~\cos \theta & -\…