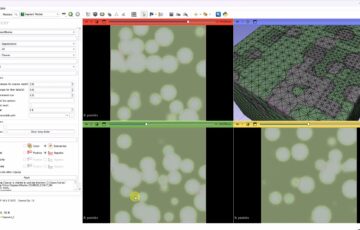
二次元平面上での物質の拡散をシミュレーションしました。三次元版はこちらにあります。
時間の経過とともにどのように物質濃度の分布が変化するかを計算します。その時に、現在の状態から⊿tだけあとの分布の状態を求めます。差分近似というものを用い、それによって得られた方程式を解いていきます。このとき、現在の状態から次の状態を求める方法が陽解法となります。他に陰解法というものがありますが、ここでは述べません。陰解法には時間増分⊿tを大きくとれるなどのメリットがあるのですが、各時間ごとに連立方程式を解く必要があり複雑です。それに比べると陽解法を使えば簡単なプログラムで拡散を計算することができます。
OpenCVによって結果を動画に出力しています。スタートは2つの大きさの異なる円盤が初期濃度1に設定されていて、それが時間の経過とともに拡散していきます。

※最後にソースコードを示してあります。
では、引き続き、今回の計算がおよそ正しいということを示していきます。
拡散方程式の陽解法によるシミュレーションのコードを用いて拡散方程式の定常解を求め、回帰を行います。
平面上への各場所の濃度φは極座標によってφ(r,θ)と表せます。今回は境界条件をr<0.05で濃度1.0、r>0.50で濃度0.0としたので、濃度分布は円対称となり、φ(r)と書きなおすことができます。解析的に定常解が求まる例なので、解析解を求めましょう。△はラプラシアンです。
拡散方程式は、∂φ/∂t=D△φと表されます。
定常解とは時間の変化があっても変化しない濃度分布のことであるので、∂φ/∂t=0が成り立ちます。すなわち、方程式D△φ=0が解ければ良いということになります。ここでDが定数の時には簡単にこれを解くことができます。
まず、2次元極座標のラプラシアンに以下の公式があります。
△=∂^2/∂x^2+∂^2/∂y^2
=(∂^2/∂r^2)+1/r(∂/∂r)+1/r^2(∂^2/∂θ^2)
これを元に、φがθによらないこと、すなわち∂^2φ/∂θ^2=0であることに注意して、
△φ=(∂^2φ/∂r^2)+1/r*(∂φ/∂r)=0
すなわち
∂^2φ/∂r^2=-1/r*(∂φ/∂r)
∂φ/∂rは微分すると-1/r倍のそれになる関数とわかり、
∂φ/∂r=A/r
これをrで積分して
φ=Alog r +B
ここに境界条件 φ(0.05)=1,φ(0.50)=0 を代入してA=-0.43 B=-0.30と求まります。
WolframAlpha {A log (0.05)+B=1, A log (0.5)+B=0}
話が少し変わりますが、 連立方程式など煩雑な計算はWolfram Alphaに任せるといいですよ。
さて、解析解とシミュレーションによって数値的に得られる解が一致するかを見て行きましょう。50万タイムステップ計算しておよそ濃度分布が収束したところでφ(r)の関数近似を行いました。エクセルで近似曲線を書きましたが、φ(r)=-0.41 log(r) – 0.30 というように求まり、それなりの精度が得られたのではないかと思います。50万タイムステップでも完全な収束には至っていないと考えられるので、それが誤差の原因の一つと考えられます。


1つ目のグラフは、時間経過による、円の直径上での濃度分布変化です。
2つ目のグラフは、ほぼ収束した後の濃度分布の対数回帰です。
今回は二次元でしたが、三次元版の拡散シミュレーションのコードも紹介しています。
#include <iostream>
#include <stdio.h>
#include "opencv/cv.h"
#include "opencv/highgui.h"
#define NMAX_X 100
#define NMAX_Y 100
#define N 2000000
double r(double,double,double,double);
double f3(double,double,int);
int main(){
cv::VideoWriter writer("kakusan.avi", CV_FOURCC_DEFAULT, 30, cv::Size(NMAX_X, NMAX_Y), true);
char *output ="noudo.txt";
FILE* fpo;
fpo=std::fopen( output, "w" );
cv::Mat img=cv::Mat(cv::Size(NMAX_X,NMAX_Y),CV_8UC3);
cv::namedWindow("img", CV_WINDOW_AUTOSIZE);
int i,j,k,p;
double ax,ay,dx,dy,dt,a;
double U[NMAX_X+1][NMAX_Y+1],UU[NMAX_X+1][NMAX_Y+1];
double MaxValue;
dt=1.0/1000000.0;
dx=1.0/(double)NMAX_X;
dy=1.0/(double)NMAX_Y;
a=1.0/10.0;
ax=1.0/dx/dx;
ay=1.0/dy/dy;
FILE* gp;
if(dt>pow((dx*dy),2)/(dx*dx+dy*dy)/2/a){
printf("dt is too big to converge\n");
return -1;
}
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
U[i][j]=f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,5);
UU[i][j]=0.0;
}
}
gp = popen("/usr/local/bin/gnuplot -persist","w");
fprintf(gp, "set terminal x11\n");
for(k=0;k<=N;k++){
if(k%500==0){
img=cv::Scalar(0,0,0);
MaxValue=0;
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
if(MaxValue<U[i][j])MaxValue=U[i][j];
}
}
for(i=0;i<=NMAX_X;i++){
for(int j=0;j<NMAX_Y;j++){
p = (int)img.step*((int)j)+(((int)i)*3);
img.data[p+1] =((int)(U[i][j]*255/MaxValue))%256 ;
}
}
cv::imshow("img", img);
writer << img;
if(cv::waitKey(1)!=-1){
fclose(fpo);
pclose(gp);
return 0;
}
printf("\n");
}
for(i=1;i<=NMAX_X-1;i++){
for(j=1;j<=NMAX_Y-1;j++){
UU[i][j]=a*dt*(ax*U[i+1][j]+ax*U[i-1][j]+ay*U[i][j+1]+ay*U[i][j-1])+(1.0-2.0*a*dt*(ax+ay))*U[i][j];
}
}
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
U[i][j]=UU[i][j];
}
}
for(i=NMAX_X/2-4;i<=NMAX_X/2+4;i++){
for(j=NMAX_Y/2-5;j<=NMAX_Y/2+5;j++){
if(f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,5))U[i][j]=1;
}
}
for(i=0;i<=NMAX_X;i++){
for(j=0;j<=NMAX_Y;j++){
if(!f3((double)i/(double)NMAX_X,(double)j/(double)NMAX_Y,50))U[i][j]=0;
}
}
if(k%10000==0){
for(int ro=0;ro<=NMAX_X;ro+=1){
fprintf(fpo, "%d %f\n",ro,U[ro][(int)NMAX_Y/2]);
printf( "%d %f\n",ro,U[ro][(int)NMAX_Y/2]);
}
fprintf(fpo, "\n\n");
fflush(fpo);
fprintf(gp, "plot ");
for(int i=0; i<=k/10000;i++){
fprintf(gp, "\"noudo.txt\" index %d using 1:2 title \"%d\" with lines,",i,i);
}
fprintf(gp, "\n");
fflush(gp);
}
}
fprintf(gp, "\n");
pclose(gp);
fclose(fpo);
}
double r(double x1,double y1,double x2,double y2){
return pow((pow((x1-x2),2)+pow((y1-y2),2)),0.5);
}
double f3(double x,double y,int rr){
if(r(x*100,y*100,50,50)<rr) return 1;
else return 0;
}