はじめに
3次元回転(金谷健一著)を読んで、あるコスト関数を最小化するための3次元回転の最適化について、リー代数の方法、の理論的なところを少なくとも一部理解したので、実際に実装してみようというのが今回の目的。
リー代数とは
無限小回転が生成する線形空間である。無限小回転の合成は、有限回転と違い、合成の順序が結果に影響を与えない(可換であるという)。
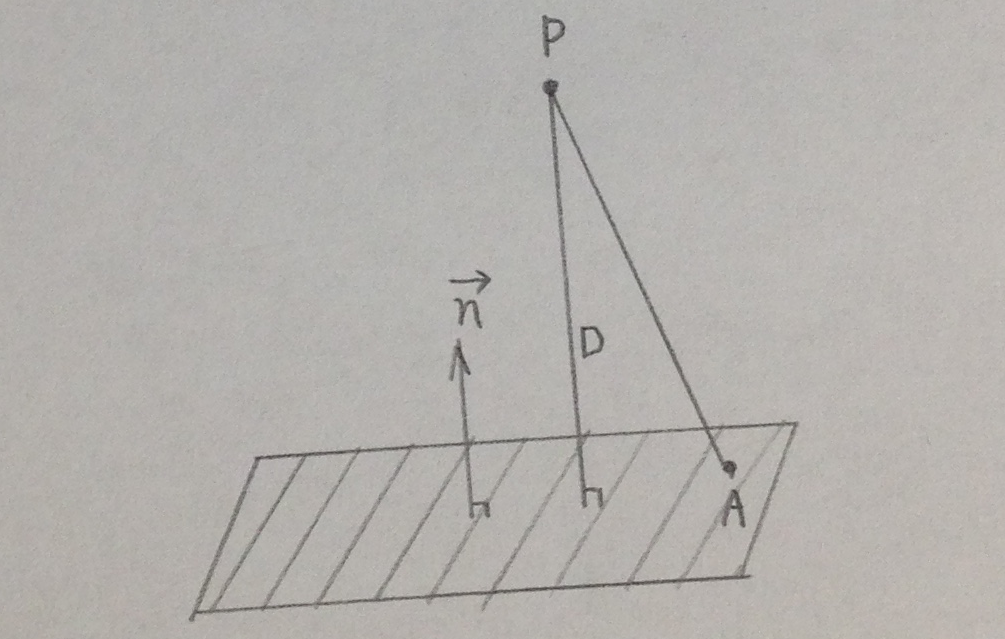
無限小回転を、有限回転に追加で合成することは、その有限回転付近での無限小回転による線形な変化を見ることである。無限小回転なので、2次以上の変化を無視しているともいえる。この無限小回転は、その有限回転において定義される接空間(接ベクトル空間)である、という。
無限小回転は、ある反対称行列Aに十分小さいdtによって、I+Adtと表現される。反対称行列は3つのパラメータで記述されるので、3つのパラメータを変化させて、有限回転の付近で最もコスト関数を最小化する方向を探し、有限回転を更新する。これを繰り返せば、コスト関数を最小化する回転が計算できる。I+Adtは厳密な回転行列ではないから、最後に得られる結果も回転行列から少し離れうる。そこで、その結果を最も近い回転行列に補正する必要がある。
Pythonでいろいろ実験してみる
無限小回転の行列
まず、無限小回転が、本当にI+Adtで表現されるのか、ということを、十分小さい角度1e-6で試してみる。
from pyquaternion import Quaternion
import numpy as np
q = Quaternion(axis=np.array([1.0, 1.0, 2.0]), angle=1e-6)
q.rotation_matrix - np.eye(3)
# 出力
array([[-4.16666701e-13, -8.16496498e-07, 4.08248457e-07],
[ 8.16496664e-07, -4.16666701e-13, -4.08248124e-07],
[-4.08248124e-07, 4.08248457e-07, -1.66644476e-13]])
確かに、Aは反対称行列(対角線は0、他は対角線を跨ぐ時に符号が入れ替わる行列)に近い。回転軸を変えても同じような結果になる。
準備:最も近い回転行列への補正
通常、フロベニウスノルムを最小化する回転行列を選択する。これは、結果として、特異値分解を行ったときに特異値をすべて1に置き換えたものと同じになる。
回転行列Rは、逆行列が転置行列になるので、それをR@R^Tが単位行列になるかを見ることでチェックできる。ここで、@はNumPyでいうところの行列積である。
まず、回転行列を崩してみる。
rot = Quaternion(axis=np.array([1.0, 1.0, 2.0]), angle=np.pi/3).rotation_matrix
rot_with_noise = rot + np.random.rand(3, 3) * 0.1
print(rot)
print(rot_with_noise)
print(rot@rot.T)
print(rot_with_noise@rot_with_noise.T)
# 出力
# 回転行列
[[ 0.58333333 -0.62377345 0.52022006]
[ 0.79044011 0.58333333 -0.18688672]
[-0.18688672 0.52022006 0.83333333]]
# 崩した回転行列
[[ 0.60881564 -0.58417763 0.56339398]
[ 0.83009892 0.61178191 -0.16292351]
[-0.15160353 0.54837406 0.88222256]]
# 回転行列のR@R^T
[[1.00000000e+00 1.78147168e-17 4.00006039e-17]
[1.78147168e-17 1.00000000e+00 4.71671236e-18]
[4.00006039e-17 4.71671236e-18 1.00000000e+00]]
# 崩した回転行列のR@R^T
[[1.02933276 0.05619777 0.08439241]
[0.05619777 1.08988539 0.0659046 ]
[0.08439241 0.0659046 1.10201438]]
rot_with_noiseでは、ノイズによってR@R^Tが確かに乱れる。
続いて、これを補正する。np.linalg.svdで特異値分解を行う。Sは、Rが十分に回転行列に近いときには単位行列になる、すなわち、特異値がすべて1になるが、回転行列でなくなるに従って、離れていく。これを単純に単位行列で置き換えて復元すると、U、Vtは直交行列なので、得られる結果は回転行列になる。
U, S, Vt = np.linalg.svd(rot_with_noise)
rot_fixed = U@Vt
print(rot_fixed)
print(rot_fixed@rot_fixed.T)
# 出力
# 補正後回転行列
[[ 0.58765643 -0.61308353 0.52800427]
[ 0.78635463 0.58643711 -0.19426247]
[-0.19054218 0.5293582 0.82672461]]
# 補正後回転行列のR@R^T
[[ 1.00000000e+00 3.10964377e-16 -4.31956114e-16]
[ 3.10964377e-16 1.00000000e+00 -5.94847355e-17]
[-4.31956114e-16 -5.94847355e-17 1.00000000e+00]]
近い値に補正され、そのR@R^Tも単位行列になる。
最適化
シンプルに最急降下法で、コスト関数を最小化してみる。
常に、最新の回転の近くで微分を計算していることに注意。微分の計算には自動微分を使っている。
import autograd.numpy as np
from autograd import grad, jacobian
def fix_rot(rot):
U, S, Vt = np.linalg.svd(rot)
rot_fixed = U@Vt
return rot_fixed
def make_A_from_w(w):
w1, w2, w3 = w
A = np.array([
[ 0, -w3, w2],
[ w3, 0, w1],
[-w2, -w1, 0]
])
return A
def cost(xyz, xyz_rotated, rot):
return np.sum((xyz_rotated - rot@xyz)**2)
n = 20
xyz = np.random.rand(3, n)
rot_gt = Quaternion(axis=np.array([1.0, 1.0, 2.0]), angle=np.pi/3).rotation_matrix
xyz_rotated = rot_gt @ xyz
rot = np.eye(3)
alpha = 0.005
for t in range(1000):
if t%10 == 0:
print("cost:", cost(xyz, xyz_rotated, rot))
def f(w):
A = make_A_from_w(w)
rot_ = (A + np.eye(3)) @ rot
return cost(xyz, xyz_rotated, rot_)
jac = jacobian(f)
w0 = np.array([0., 0., 0.])
j = jac(w0)
A = make_A_from_w(-j * alpha)
rot = (A + np.eye(3)) @ rot
rot = fix_rot(rot)
# 出力
cost: 3.9702549344251628
cost: 1.6704174593991687
cost: 1.0027392982419492
cost: 0.6002849027408019
cost: 0.35364862052704077
cost: 0.20625092594736405
cost: 0.11962215280830635
cost: 0.06921272409593454
cost: 0.04004941308338197
cost: 0.023234351825969623
:
:
cost: 0.0004929792016906296
cost: 0.0004929792016906142
cost: 0.0004929792016906262
cost: 0.0004929792016905991
結果は、正解が
array([[ 0.58333333, -0.62377345, 0.52022006],
[ 0.79044011, 0.58333333, -0.18688672],
[-0.18688672, 0.52022006, 0.83333333]])
に対して、
array([[ 0.58931866, -0.62918377, 0.52054695],
[ 0.79657117, 0.58803591, -0.19202649],
[-0.18970697, 0.52627442, 0.83512569]])
が計算された。ひとまず上手くいっているようである。