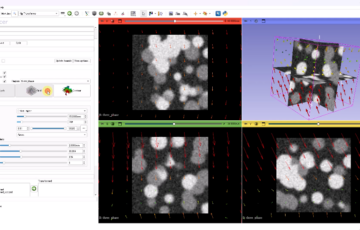
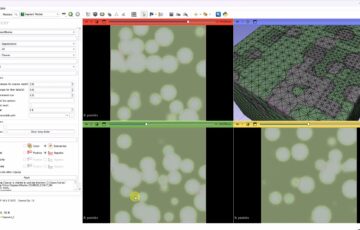
今回は干潟を斜め上の角度から撮影した画像をオリジナル画像とし、ホモグラフィー変換によって真上から撮影したような形状に変形する例を紹介します。

平面の変形方法にはいくつか種類がありますが、透視変換(ホモグラフィー変換)は最も上位に位置する変換方法です。オリジナルの長方形があったときに、Translation:平行移動とEuclidian:回転までは形自体は変わりません。アフィン変換は平行四辺形に変形できますが、辺同士の平行の関係は維持されます。それに対し、ホモグラフィー変換は自由に変形することができる変換手法です。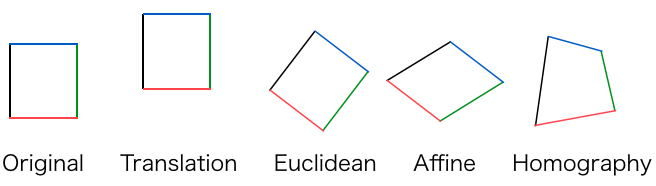
ホモグラフィー変換では、変換前と変換後で対応する4点を指定すると一意の変換を指定することになります。
下の画像はオリジナル画像の変換前の4点を赤丸でマークしたものです。緑色の線は変換前の四角形を示す線です。今回はこの四角形を正方形に変換したいと思います。

変換後の画像です。


細かな定義や原理を知らなくても変換自体は行えます。ところで、透視変換という変換方法はAdobe Premiere Proで言うところの「コーナーピン」に相当します。この機能は、画像を3次元空間に貼り付けたように見せる機能です。実は上の写真は私が高校生のときにハクセンシオマネキという小さな白いカニの生態調査で撮影したものです。カメラを設置し、カニを撮影するのですが、斜め上から撮影した動画を透視変換して、ちょうど真上から撮影したかのような動画に変形する必要がありました。当時はOpenCVで透視変換ができるだけの技量がなかったので、Adobe Premiere Proの30日無料体験期間を使って変形していました。それが、OpenCVで完全にフリーでできるというのは今になって驚きです。
#include "opencv/cv.h"
#include "opencv/highgui.h"
using namespace cv;
const int WIDTH = 600;
const int HEIGHT = 600;
int main()
{
Mat src = imread( "field.png" );
Mat dst= Mat::zeros(HEIGHT+100, WIDTH+100, CV_8UC3);
// 1 3
//
// 2 4
// 変換前の画像での座標
const Point2f src_pt[]={
Point2f(360 , 69 ),
Point2f(85 , 602),
Point2f(1032, 79 ),
Point2f(1198, 631)};
// 変換後の画像での座標
const Point2f dst_pt[]={
Point2f(50, 50 ),
Point2f(50, 50+HEIGHT - 1),
Point2f(50+WIDTH - 1, 50 ),
Point2f(50+WIDTH - 1, 50+HEIGHT - 1)};
// homography 行列を計算
const Mat homography_matrix = getPerspectiveTransform(src_pt,dst_pt);
// 透視変換
warpPerspective( src, dst, homography_matrix, dst.size());
imshow("result", dst);
imwrite("field_out.png", dst);
waitKey();
return 0;
}