クロフトンの公式
CTなどのボリュームデータにおいて、何らかの方法でセグメンテーションを行ったあと、そのラベルデータの表面積を計算したいときがあります。このとき、クロフトンの公式というものを使うと正確に計算できます。これを使わない方法としては、マーチングキューブ法などを使って表面を三角形の集合として構成し、表面積をそれらの面積の合計で計算する方法もありますが、一般的にクロフトンの公式で求めた表面積のほうが正確です。
ロジックは、いきなり3次元で考えると難しいので、手始めに2次元で考えてみましょう。単位円に対してX軸に並行な線を等間隔にたくさん交差させてみます。

同じように、他の角度からも線を引いていきます。直感としては、円がもっと複雑な形になり、周の長さが増えると、交差回数が増えそうです。このとき、各方向から引いた線と円の交差する回数の平均を計算すると、周の長さに比例します。この法則は、実は円でなくても成り立ち、2次元における周の長さ、3次元における表面積を求めるために使えます。クロフトンの公式と呼ばれ、理論的な裏付け(Wikipedia)があります。
理論的には、無限の種類の方向から並行な線を生成する必要がありますが、離散的に表現されたデータの表面積を計算する際には、2次元のとき4方向、3次元のとき13方向から、生成すると十分な精度の値が得られることがわかっています。
2次元のグリッドに格納されたデータであれば、8近傍のうち対称性から2で割って4方向(縦1/横1/斜め2)、3次元のグリッドに格納されたデータであれば、これも同様に26近傍/2で13方向です。
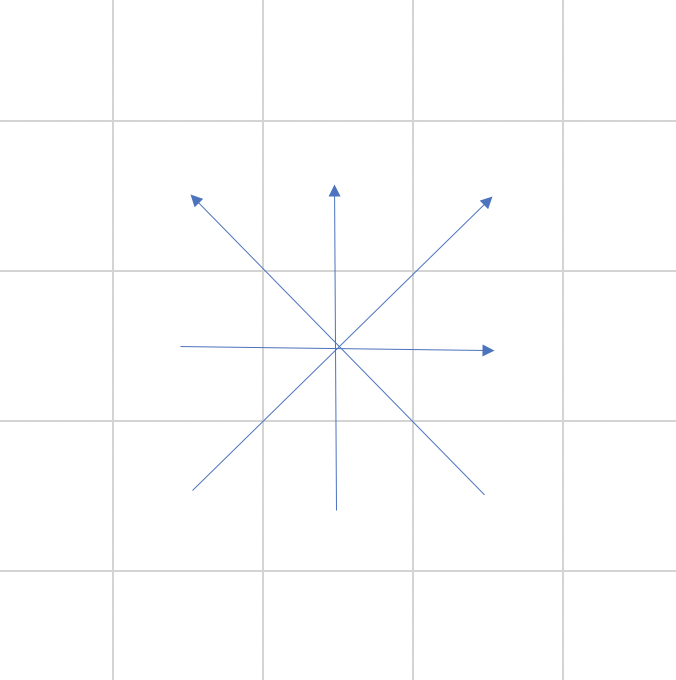
2次元の場合の4つの方向
Python/NumPyによる実装
まず、3次元のNumPy配列を生成し、半球内部を1にマークしたデータをサンプルとして作成します。
import numpy as np
import matplotlib.pyplot as plt
data = np.zeros((101,101,101), dtype=np.uint8)
for x in range(data.shape[0]):
for y in range(data.shape[1]):
for z in range(data.shape[2]):
if (x-50)**2+(y-50)**2+(z-50)**2 < 50**2 and z < 50.5:
data[x,y,z] = 1
plt.imshow(data[:, 50, :])
plt.show()

次に、クロフトンの公式に従って、13方向分の交差回数をカウントし、表面積を計算しています。交差回数のカウントには、方向によって$1$, $2^{0.5}$, $3^{0.5}$の重みをつけます。もし対象のデータが異方性ボクセルデータ(XYZでボクセルサイズが違うデータ)の場合には、この係数が変わります。
具体的には、ボクセルサイズが等しい場合、カウントを$1$, $2^{0.5}$, $3^{0.5}$で割っていますが、これは、比率としては、その交差方向における交差点の平均間隔です。したがって、ボクセルサイズが異なる場合は、例えば1, 2, 3の辺の長さを持つ場合、同様に方向によって、1, 2, 3 , ((1^2)+(2^2))^0.5, ((1^2)+(3^2))^0.5, ((3^2)+(2^2))^0.5, ((1^2)+(2^2)+(3^2))^0.5 で割れば、比率としてはよいです。その上で、ボクセルサイズが大きくなると1つの交差あたりが表現する表面積も増えるため、この比率に一律に3辺の長さの積 = 6をかけます。すると次元としては、長さ^-1 * 体積 = 面積 の次元となり、次元の観点からも辻褄が合うのがわかると思います。 参考文献: On the Analysis of Spatial Binary Images
ここでは、高速化のために、斜め方向にグリッドの値を一つづつ取得するようなことはせず、np.rollによって、最初にまとめてずらしています。こうすることにより、軸に沿ったNumPyの並列化された高速な演算が利用可能になります。rollすると、一例として次の図のように斜めに画素がずれていきます。

このとき、np.rollでずらしたときに、境界の位置を区別する実装を不要とするために、事前に周辺に0のpaddingを入れておくと便利です。
padded = np.pad(data, 1, 'constant', constant_values=0)
次の式で、axis1に沿った方向に関して、何回0/1の反転があったかを計算しています。np.diffは0->1の反転があったところで+1、逆の反転があったところで-1を返してくれます。
diff = np.abs(np.sign(np.diff(rolled, axis=axis1)))
それを絶対値をとってから、合計します。
cross_section = np.sum(diff) * (2**-0.5)
関数としてまとめると、全体としては次のようになります。
from copy import deepcopy
import numpy as np
data = np.zeros((101,101,101), dtype=np.uint8)
for x in range(data.shape[0]):
for y in range(data.shape[1]):
for z in range(data.shape[2]):
if (x-50)**2+(y-50)**2+(z-50)**2 < 50**2 and z < 50.5:
data[x,y,z] = 1
def crofton_surface(data):
padded = np.pad(data, 1, 'constant', constant_values=0)
cross_section_sum = 0
# along axis X, Y, Z
for axis in [0, 1, 2]:
diff = np.abs(np.sign(np.diff(padded,axis=axis)))
cross_section = np.sum(diff)
cross_section_sum += cross_section
# along axis XY, YZ, ZX, -XY, -YZ, -ZX
for axis1 in [0, 1, 2]:
for axis2 in [0, 1, 2]:
if axis1 >= axis2:
continue
for sgn in [1, -1]:
rolled = deepcopy(padded)
for i in range(padded.shape[axis1]):
slicer = tuple([(slice(None) if j != axis1 else [i]) for j in range(3)])
rolled[slicer] = np.roll(rolled[slicer], i*sgn, axis=axis2)
diff = np.abs(np.sign(np.diff(rolled, axis=axis1)))
cross_section = np.sum(diff) * (2**-0.5)
cross_section_sum += cross_section
# along axis XYZ, XY-Z, X-Y-Z, X-YZ
rollsgn = [
[1, 1],
[1, -1],
[-1, 1],
[-1, -1]
]
for sgns in rollsgn:
rolled = deepcopy(padded)
for i in range(padded.shape[0]):
rolled[[i], : , :] = np.roll(rolled[[i], : , :], i*sgns[0], axis=1)
rolled[[i], : , :] = np.roll(rolled[[i], : , :], i*sgns[1], axis=2)
diff = np.abs(np.sign(np.diff(rolled, axis=0)))
cross_section = np.sum(diff) * (3**-0.5)
cross_section_sum += cross_section
crofton_s = cross_section_sum / 13 * 2
return crofton_s
print(crofton_surface(data))
計算される値は、23134.45148512964となります。理論値は23561.94490192345ですので、-1.8%くらいの誤差です。ただし、この誤差は、この場合だと半球をグリッドデータで表現しきれなかったことによる離散化を原因として生じています。つまり、半球の半径を大きくすると相対的にグリッドデータで良く近似できるようになるため誤差は小さくなり、逆もまた然りです。言い換えると、解像度が低いと球の形状を正確に表現できないため、表面積の計算精度も下がる、逆もまた然り、ということです。また、これは、後述するように精度を過小評価しています。本当の精度はもっと良いです。
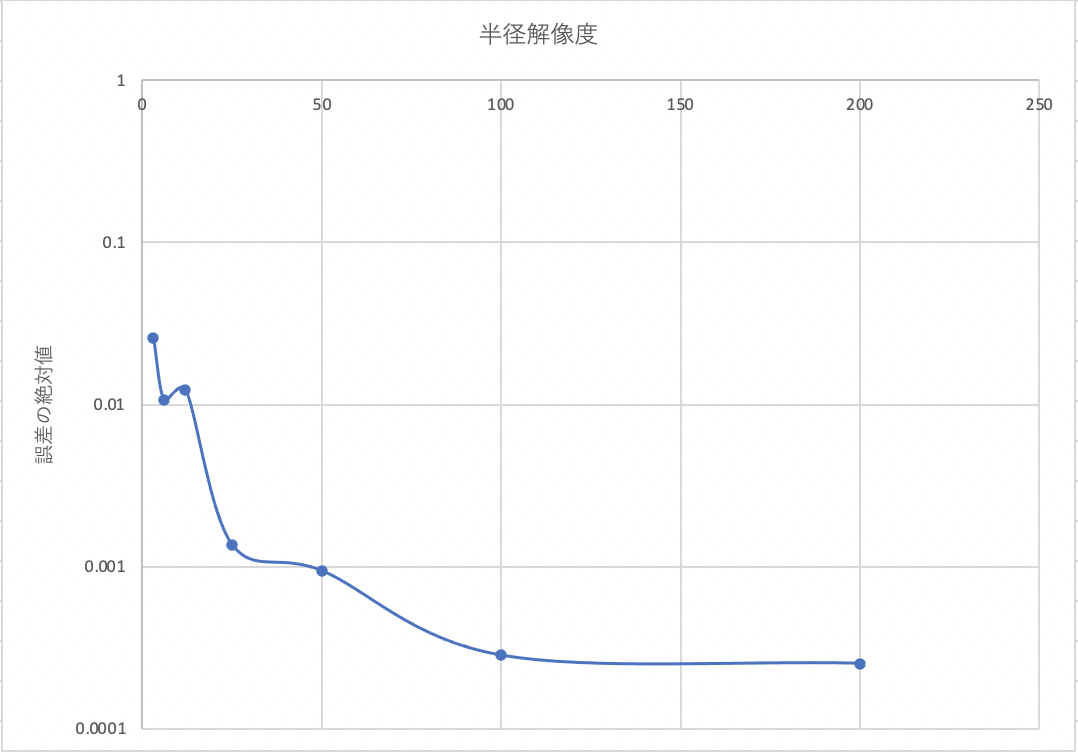
精度の評価:全球を対象とした、解像度と理論値との誤差の関係
ここでは、解像度が上がると、クロフトンの公式で得られる表面積の精度が上昇することを示します。
for resolution in [3, 6, 12, 25, 50, 100, 200]:
s = resolution * 2 + 1
data = np.zeros((s,s,s), dtype=np.uint8)
for x in range(data.shape[0]):
for y in range(data.shape[1]):
for z in range(data.shape[2]):
if (x-resolution)**2+(y-resolution)**2+(z-resolution)**2 < resolution**2:
data[x,y,z] = 1
ref_r = (np.sum(data) / (4 / 3 * np.pi))**(1/3)
ref_val = ref_r * ref_r * 4 * np.pi
crofton_val = crofton_surface(data)
print(resolution, crofton_val / ref_val - 1)
| 半径解像度 | 誤差 |
|---|---|
| 3 | -0.025749434252466452 |
| 6 | -0.010600119437024547 |
| 12 | -0.012273578514940486 |
| 25 | -0.0013569220234589396 |
| 50 | -0.0009411365552849382 |
| 100 | -0.0002839355496748741 |
| 200 | -0.0002531280824736859 |
なぜ、ref_rを計算しているかというと、特に解像度が小さいときに、ボクセルグリッド表現だと球とは大きく異なった表現になりやすいからです。そのため、生成されたグリッド表現の体積を計算し、そこから逆算して半径を計算し直しています。その半径を使って表面積の理論値ref_valを計算して比較に使っています。
その点、半球での-1.8%という誤差は、すこしクロフトンの公式に従った表面積計算の能力を過小評価しています。本来なら、ここでわかるように、半径が50マスで表現されるグリッドデータ表現の場合、-0.09%の誤差で計算できます。ただし、一貫して小さめに計算されているのがわかると思います。これは、真球表面の曲率は厳密に1/rであるのに対し、クロフトンの公式では13方向から交点を計算する都合上、表面をボクセルのレベルまで拡大すると曲率はゼロになるためです。簡単にいうと球のほうが膨らみがある分、表面積が大きくなります。
また、この結果からは、小さいボクセル集合で形成されるボリュームに関しては、表面積の計算が難しい、ということも分かります。考えてみれば当たり前ですが、例えばCTデータにおいて、1ボクセルで観測された輝点が球なのか、それとも立方体なのか、はたまた別の形なのかは、情報が得られないわけですから、これは解決が難しい問題です。