回転の平均、回転同士の距離

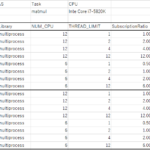
自分用のメモです。回転同士の距離がどういうものか、といったことはここに日本語で詳しく書いてあります(とても良いページ!)。

from pyquaternion import Quaternion
import numpy as np
qlist = [Quaternion.random().elements for i in range(10)]
mlist = [q.rotation_matrix for q in qlist]

クオータニオン

平均

クオータニオンの列があったとき、新しいクオータニオンひとつを考える。このクオータニオンとクオータニオン列との内積の和が最小になるようにすれば、平均クオータニオンが計算される。実際には、クオータニオン列をNx4の行列Xにしてしまい、X.T・X (4×4行列)の最大の固有ベクトルを求めればよい。

def mean_q(qlist):
    x = np.array([q.elements for q in qlist])
    m = x.T @ x
    w, v = np.linalg.eig(m)
    return Quaternion(v[:, np.argmax(w)])

距離

内積をとってarccosして、2倍する、と、クオータニオン間の角度として距離が計算できる。

def dist_q(q1, q2):
    return 2 * np.arccos(np.dot(q1.elements, q2.elements))

3×3行列

平均

いろいろ調べているが、いまのところ見つけていない。クオータニオンを経由すれば計算できる。。

距離

クオータニオンの方で求めたものと対応する角度として距離が計算できる。

def dist_m(m1, m2):
    return np.arccos((np.trace(m1 @ m2.T) - 1) / 2)