OpenCVでフーリエ変換

C++とOpenCVを使ってフーリエ変換を行います。フーリエ変換はJPEGの圧縮にも使われる技術ですが、ノイズの除去などにも応用が可能です。

まず、フーリエ変換についてですが、フーリエ変換は元の画像あるいは波形から、それを構成するsin波の周波数成分を取り出すことを意味します。すなわち、ある波形があるとして、それが簡単な波の合成と見たときに各々の波の周波数を取り出すということです。

↑「道具としてのフーリエ解析」より、フーリエ変換の模式図。

実は、滑らかな変化をする関数は全て波の合成で表すことができるという事実の上にフーリエ変換が成り立っているのですが、その辺りの証明などについてはここでは触れません。2次元の場合には、下図のような波になります。

z=sin(5x)*sin(3y)

 

なぜ、フーリエ変換を画像処理、画像解析の分野で扱うのかというと、おもに、ノイズ除去や画像圧縮に用いられるためです。実は、フーリエ変換で周波数を取り出すと、周波数と各周波数ごとの振幅の組み合わせから元のデータを復元できます。これを逆フーリエ変換と言います。つまり、うまくやると、データ量を圧縮できるのです。圧縮率によりますが、JPEGなどの画像形式ではフーリエ変換を行い、見た目には影響を与えにくい部分の周波数帯の情報をカットすることにより、ほとんど画質を劣化させずに元の10分の1以下のデータサイズに圧縮することができます。また、ノイズ除去に関しては、周波数と振幅の組み合わせからデータを復元できるので、フーリエ変換した結果からノイズに相当する周波数の振幅をゼロにして、逆フーリエ変換を行えばノイズが除去できるということになります。

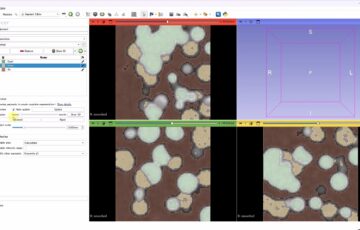
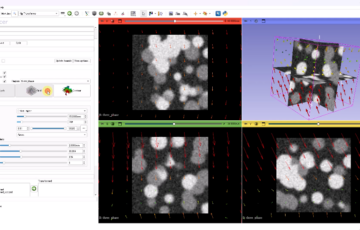
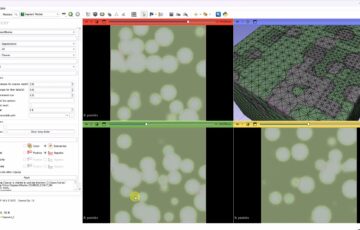
今回は、OpenCVを用いて、画像に対してフーリエ変換と逆フーリエ変換を行うコードを紹介します。いつもより難しいと思いますので、ちょっと試したいという人ならコピペでもいいかもしれません。下の例では、顕微鏡で細胞を撮影したものを元画像にしています。核と細胞膜が写っていますが、高周波数部分をゼロにすることで核をマスクすることに成功しています。これは核が高周波の成分で構成されていたためです。

#include "opencv/cv.h"
#include "opencv/highgui.h"
using namespace cv;

void shiftDft(Mat &src, Mat &dst)
{
    Mat tmp;
    
    int cx = src.cols/2;
    int cy = src.rows/2;
    
    for(int i=0; i<=cx; i+=cx) {
        Mat qs(src, Rect(i^cx,0,cx,cy));
        Mat qd(dst, Rect(i,cy,cx,cy));
        qs.copyTo(tmp);
        qd.copyTo(qs);
        tmp.copyTo(qd);
    }
}

Mat encodeImage(Mat &src){
    Mat Re_img, Im_img, Complex_img, dft_src, dft_dst, dft_dst_p, mag_img;
    vector<Mat> mv;
    
    Size s_size = src.size();
    Re_img = Mat(s_size, CV_64F);
    Im_img = Mat::zeros(s_size, CV_64F);
    Complex_img = Mat(s_size, CV_64FC2);
    
    src.convertTo(Re_img, CV_64F);
    mv.push_back(Re_img);
    mv.push_back(Im_img);
    merge(mv, Complex_img);
    
    int dft_rows = getOptimalDFTSize(src.rows);
    int dft_cols = getOptimalDFTSize(src.cols);
    
    dft_src = Mat::zeros(dft_rows, dft_cols, CV_64FC2);
    
    Mat roi(dft_src, Rect(0, 0, src.cols, src.rows));
    Complex_img.copyTo(roi);
    
    dft(dft_src, dft_dst);
    shiftDft(dft_dst, dft_dst);
    return dft_dst;
}

Mat decodeImage(const Mat dft_dst){
    Mat dft_src, idft_img;
    vector<Mat> mv;
    double min, max;
    
    Mat dft_dst_clone=dft_dst.clone();
    shiftDft(dft_dst_clone, dft_dst_clone);
    
    idft(dft_dst_clone, dft_src);
    split(dft_src, mv);
    minMaxLoc(mv[0], &min, &max);
    idft_img = Mat(mv[0]*1.0/max);
    
    return idft_img;
}

Mat genMagImage(const Mat dft_dst){
    Mat mag_img;
    vector<Mat> mv;
    split(dft_dst, mv);
    
    magnitude(mv[0], mv[1], mag_img);
    log(mag_img+1, mag_img);
    normalize(mag_img, mag_img, 0, 1, CV_MINMAX);
    return mag_img;
}

int main(){
    Mat src_img = imread("sample.png", IMREAD_GRAYSCALE);
    Mat mag_img;
    
    Mat dft_dst=encodeImage(src_img);
    
    Mat mask=Mat::ones(dft_dst.size(),CV_8UC1)*255;
    circle(mask, cv::Point(dft_dst.cols/2, dft_dst.rows/2), 9, Scalar(0), -1, 4);
    imshow("mask",mask);
    
    Mat dft_dst_mask;
    dft_dst.copyTo(dft_dst_mask,mask);
    
    imshow("before",src_img);
    imshow("mag",genMagImage(dft_dst_mask));
    imshow("after",decodeImage(dft_dst_mask));
    
    waitKey(0);
    return 0;
}